Now, let's look closer at these electron orbitals and their shapes. Remember, we used a two-dimensional plot of the wave function versus x to visualize the standing wave of an electron trapped in one dimension. To visualize the standing waves (or orbitals) of electrons bound to a positively charged nucleus in three dimensions, we will need a four-dimensional plot of the wave function vs. x, y, and z. This can be a bit tricky since our visual perception is limited to three spatial dimensions. So we will need a few tricks to help us visualize the four-dimensional standing waves of the electron in 3 dimension.
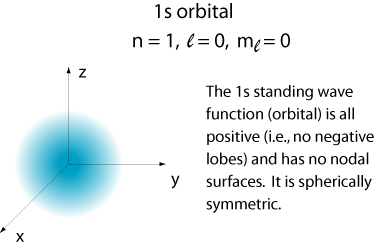
1s-orbital:
The lowest energy orbital of the hydrogen atom.
2s-orbital:
The second harmonic state.

Remember that at the node, the probability of finding the electron is zero. In general, an orbital with high n (principal quantum number) (e.g. n = 2, 3, 4...) means that the electron will extend out from the nucleus further, and so will be held less tightly than a 1s electron.
2p-orbital:
When n = 2, we have 2 possible values for ℓ. The first is ℓ = 0, or 2s orbital, which we just discussed above. The second possibility is ℓ = 1 or the 2 p orbital. For a given value of ℓ there are 2 ℓ + 1 possible ml values. So for ℓ = 1, we have mℓ= -1, 0, +1. These three values of mℓ correspond to three different p-orbitals.

P-orbitals look like dumbbells along each axis. Instead of a radial node, we have an angular node, which lies along the plane perpendicular to the axis in which the orbital lies. Since the energy, E, of each orbital is a function of only n, then all the n = 2 orbitals (2s, 2px, 2py, 2pz) have the same energy.
n = 3 orbitals:
For the n=3 orbitals the possible quantum numbers are:
| n=3 | ℓ=0 | mℓ=0 | 3s orbital |
| n=3 | ℓ=1 | mℓ=-1, 0, +1 | 3p orbitals |
| n=3 | ℓ=2 | mℓ=-2, -1, 0, +1, +2 | 3d orbitals |
For much nicer three-dimensional renderings of all the atomic orbitals visit Mark Winter's Orbitron site .
Homework from Chemisty, The Central Science, 10th Ed.
6.49, 6.51, 6.53, 6.55, 6.57

